线性代数(Linear Algebra)学习笔记
向量(Vectors)
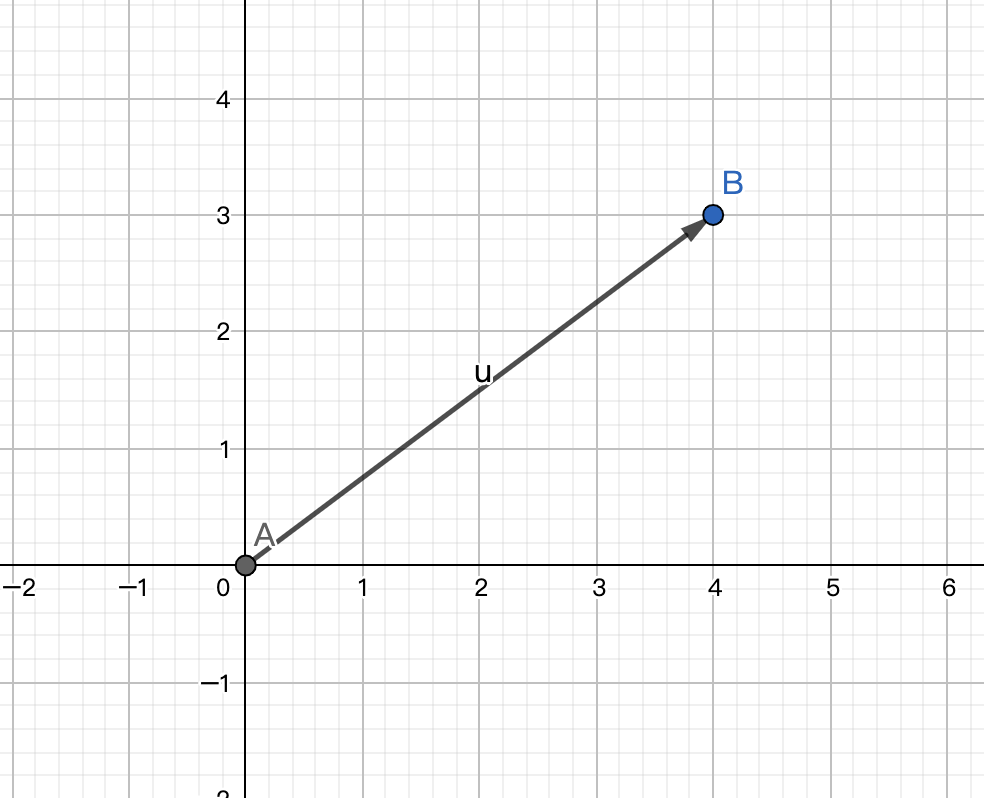
在空间中,向量可以表示为一个有方向有长短的箭头。(数学中的向量为自由向量,是没有起点的。在线性代数中,通常使向量的起点为原点,此图以二维为例)
在运算时,因为线性代数中向量以原点为起点,所以用中括号扩起来的竖着写的坐标表示一个从原点指向终点(a,b)的向量。(以二维为例)
[ a b ] \begin{bmatrix}
a\\
b
\end{bmatrix}
[ a b ]
这里的a a a b b b x x x a a a y y y b b b
向量的基础运算
向量加法(Vector Addition)
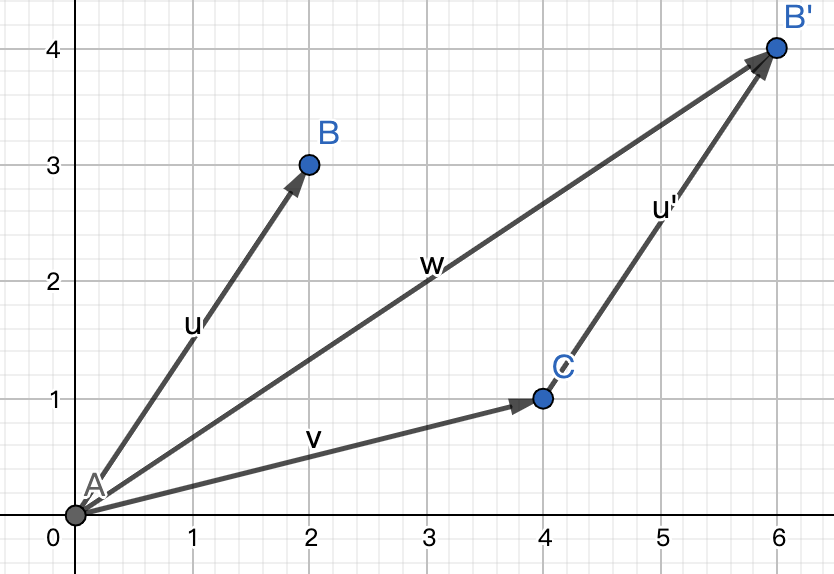
两个向量之间的加法遵从三角形法则 ,即将一个向量u ⃗ \vec{u} u v ⃗ \vec{v} v v ⃗ \vec{v} v u ⃗ \vec{u} u u ⃗ \vec{u} u v ⃗ \vec{v} v w ⃗ \vec{w} w
或者,我们将u ⃗ \vec{u} u [ a b ] \begin{bmatrix} a\\ b \end{bmatrix} [ a b ] v ⃗ \vec{v} v [ c d ] \begin{bmatrix} c\\ d \end{bmatrix} [ c d ]
因为向量可以表示为从起点向终点的移动,所以我们也可以把向量加法理解为先向x x x a + c a + c a + c y y y b + d b + d b + d w ⃗ \vec{w} w [ a + c b + d ] \begin{bmatrix} {a + c}\\ {b + d} \end{bmatrix} [ a + c b + d ]
[ a b ] + [ c d ] = [ a + c b + d ] \begin{bmatrix} a\\ b \end{bmatrix} + \begin{bmatrix} c\\ d \end{bmatrix} = \begin{bmatrix} {a + c}\\ {b + d} \end{bmatrix}
[ a b ] + [ c d ] = [ a + c b + d ]
向量数乘(Multiplication Of Vector By Scalar)
向量数乘表示向量与一个标量相乘。对于标量n n n n u ⃗ n\vec{u} n u u ⃗ \vec{u} u ∣ n ∣ |n| ∣ n ∣ n < 0 n < 0 n < 0 ∣ n ∣ |n| ∣ n ∣ 向量的缩放 ,用于缩放向量的量称之为标量(Scalars) 。因为数字在线性代数中起到的主要作用是缩放向量,所以通常“标量”与“数字”两个词在这里可以互相替换。因为向量可以理解为起点到终点的移动,所以数乘也可以表示为移动格数的缩放:
n ⋅ [ x y ] = [ n x n y ] n·\begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} {n x} \\ {n y} \end{bmatrix}
n ⋅ [ x y ] = [ n x n y ]
基向量
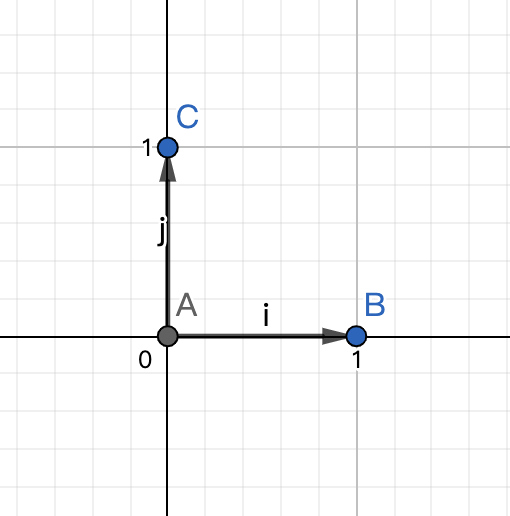
对于平面中的向量[ 3 2 ] \begin{bmatrix} 3\\ 2 \end{bmatrix} [ 3 2 ] x O y xOy x O y i ^ \hat{i} i ^ j ^ \hat{j} j ^ i ^ \hat{i} i ^ x x x x x x j ^ \hat{j} j ^ y y y y y y [ 3 2 ] \begin{bmatrix} 3\\ 2 \end{bmatrix} [ 3 2 ] i ^ \hat{i} i ^ j ^ \hat{j} j ^ i ^ \hat{i} i ^ j ^ \hat{j} j ^ 基向量 (Basis Vectors)。(基向量的严格定义——张成该空间的一个线形无关向量的集合,下文会讲线形无关。)
张成空间
所以我们可以用任意两个不共线的向量来表示一个坐标系。
我们选取向量u ⃗ \vec{u} u v ⃗ \vec{v} v w ⃗ = x u ⃗ + y v ⃗ \vec{w}=x\vec{u}+y\vec{v} w = x u + y v u ⃗ \vec{u} u v ⃗ \vec{v} v w ⃗ \vec{w} w 给定向量的张成空间(The Span Of Those Vectors) 。
线性组合
像上文中,两个向量数乘之和的结果被称之为向量的线形组合(Linear Combinations) 。在三维空间中,两个不共线向量所张成的空间为一个平面,而我们再添加一个向量,如果这个向量在前两个向量所张成的平面内,它并不会改变张成空间的大小;可如果随机选择一个向量,它几乎不会落在前两个向量所张成的平面内,这时候由这三个向量所张成的空间就包含了所有的三维变量,如果我们操纵第三个向量的缩放,它就会操控着前两个向量所张成的平面扫过整个空间。
如果有一个向量w ⃗ \vec{w} w u ⃗ \vec{u} u v ⃗ \vec{v} v w ⃗ = a u ⃗ + b v ⃗ \vec{w}=a\vec{u}+b\vec{v} w = a u + b v 线性相关(Linearly Dependent)
如果所有向量都使张开的空间增加了新的维度,则称w ⃗ ≠ a v ⃗ \vec{w}\not=a\vec{v} w = a v 线形无关(Linearly Independent) (a取所有值)。
线性变换
变换可以理解为更直观的、可视化的函数,我们可以想象一个向量的变换、一组向量终点的变换甚至一整个平面的变换。在线性代数中,变换限制在一种很特殊的类型中:线性变换(Linear Transformations) 。如果一个变换满足如下两个性质,则称它是线形的:
直线在变化后仍保持为直线,不能有所弯曲
原点必须保持固定
线形变换是一种操纵空间的手段,我们也可以把线性变换看作是“保持网格线等距分布”的变换。
矩阵
矩阵的定义
因为平面中所有的向量均可以用基向量数乘的和来表示,所以我们只需要知道基向量i ^ \hat{i} i ^ j ^ \hat{j} j ^
i ^ \hat{i} i ^ [ 1 3 ] \begin{bmatrix} 1\\ 3 \end{bmatrix} [ 1 3 ] j ^ \hat{j} j ^ [ − 2 0 ] \begin{bmatrix} -2\\ 0 \end{bmatrix} [ − 2 0 ] [ x y ] \begin{bmatrix} x\\ y \end{bmatrix} [ x y ]
[ x y ] → x [ 1 3 ] + y [ − 2 0 ] = [ 1 x + ( − 2 ) y 3 x + 0 y ] \begin{bmatrix} x\\ y \end{bmatrix} \rightarrow x\begin{bmatrix} 1\\ 3 \end{bmatrix} + y\begin{bmatrix} -2\\ 0 \end{bmatrix} = \begin{bmatrix} {1x + (-2)y}\\ {3x + 0y} \end{bmatrix}
[ x y ] → x [ 1 3 ] + y [ − 2 0 ] = [ 1 x + ( − 2 ) y 3 x + 0 y ]
通过这个过程,我们可以将任意一个向量的变化计算出来,所以一个二维现象变换仅有四个数字就可以完全确定:变化后的基变量i ^ \hat{i} i ^ j ^ \hat{j} j ^
通常我们将它们变化后的坐标放入一个2 × 2 2\times2 2 × 2 2 × 2 2\times2 2 × 2 2 × 2 2\times2 2 × 2 [ 1 − 2 3 0 ] \begin{bmatrix} 1 & {-2}\\ 3 & 0 \end{bmatrix} [ 1 3 − 2 0 ]
矩阵向量乘法与变换
所以对于一个矩阵[ a b c d ] \begin{bmatrix} a & b\\ c & d \end{bmatrix} [ a c b d ] [ x y ] \begin{bmatrix} x\\ y \end{bmatrix} [ x y ]
[ a b c d ] [ x y ] = x [ a c ] + y [ b d ] = [ a x + b y c x + d y ] \begin{bmatrix} a & b\\ c & d \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix}=x\begin{bmatrix} a\\ c \end{bmatrix} + y\begin{bmatrix} b\\ d \end{bmatrix} = \begin{bmatrix} {ax + by}\\ {cx + dy} \end{bmatrix}
[ a c b d ] [ x y ] = x [ a c ] + y [ b d ] = [ a x + b y c x + d y ]
中间的部分直观的展示了向量的变化情况。
有一个有意思的变换,变换中 i ^ \hat{i} i ^ [ 1 0 ] \begin{bmatrix} 1\\ 0 \end{bmatrix} [ 1 0 ] j ^ \hat{j} j ^ [ 1 1 ] \begin{bmatrix} 1\\ 1 \end{bmatrix} [ 1 1 ] [ 1 1 0 1 ] \begin{bmatrix} 1 & 1\\ 0 & 1 \end{bmatrix} [ 1 0 1 1 ] 剪切(Shear) 。
如果变化后的i ^ \hat{i} i ^ j ^ \hat{j} j ^ 列线性相关(Lineary Dependent Columns) 。
矩阵乘法与线形变换复合
矩阵乘法定义
有时我们想描述一个变化之后再进行另一个变化,这个新的线形变换就称为前两种变换的复合变换(Composition) 。和一般的变换一样,我们也可以通过i ^ \hat{i} i ^ j ^ \hat{j} j ^
[ a b c d ] [ e f g h ] = [ ? ? ? ? ] \begin{bmatrix} a & b\\ c & d \end{bmatrix} \begin{bmatrix} e & f\\ g & h \end{bmatrix}=\begin{bmatrix} &?&&&?&\\ &?&&&?& \end{bmatrix}
[ a c b d ] [ e g f h ] = [ ? ? ? ? ]
因为矩阵第一列为变化后的 i ^ \hat{i} i ^ j ^ \hat{j} j ^
i ^ → [ a b c d ] [ e g ] = e [ a c ] + g [ b d ] = [ a e + b g c e + d g ] \hat{i}\rightarrow\begin{bmatrix}a & b\\ c & d \end{bmatrix} \begin{bmatrix}e\\ g\end{bmatrix}=e\begin{bmatrix}a\\c\end{bmatrix}+g\begin{bmatrix}b\\d\end{bmatrix}=\begin{bmatrix}ae+bg\\ce+dg\end{bmatrix}
i ^ → [ a c b d ] [ e g ] = e [ a c ] + g [ b d ] = [ a e + b g ce + d g ]
j ^ → [ a b c d ] [ f h ] = f [ a c ] + h [ b d ] = [ a f + b h c f + d h ] \hat{j}\rightarrow\begin{bmatrix}a & b\\ c & d \end{bmatrix} \begin{bmatrix}f\\ h\end{bmatrix}=f\begin{bmatrix}a\\c\end{bmatrix}+h\begin{bmatrix}b\\d\end{bmatrix}=\begin{bmatrix}af+bh\\cf+dh\end{bmatrix}
j ^ → [ a c b d ] [ f h ] = f [ a c ] + h [ b d ] = [ a f + bh c f + d h ]
所以两个矩阵的乘积为:
[ a b c d ] [ e f g h ] = [ a e + b g a f + b h c e + d g c f + d h ] \begin{bmatrix} a & b\\ c & d \end{bmatrix} \begin{bmatrix} e & f\\ g & h \end{bmatrix}=\begin{bmatrix} ae+bg&af+bh\\ ce+dg&cf+dh \end{bmatrix}
[ a c b d ] [ e g f h ] = [ a e + b g ce + d g a f + bh c f + d h ]
当两个变化相继发生时,变化发生的顺序影响最后的效果,所以矩阵相乘时,矩阵的先后顺序对结果有影响(M 1 M 2 ≠ M 2 M 1 M_1M_2\not=M_2M_1 M 1 M 2 = M 2 M 1
矩阵乘法结合律(Associativity)
有矩阵A、B、C,问这三个矩阵相乘时是否能够在保证相互顺序不变的情况下进行结合[( A B ) C = A ( B C ) (AB)C=A(BC) ( A B ) C = A ( BC )
如果分别设这三个矩阵为四个未知量进行计算,这个过程的计算量会相当的庞大并且只是无意义的计算,所以我们不妨用更巧妙的变换的思想来解决这个问题。通过对平面进行变换,我们可以发现这个矩阵乘法是满足结合律的,这个方法更加直观与简洁,而且这确实是一个实实在在的证明,并能解释为什么是正确的。